[백준 2749][C++] 피보나치 수 3

문제

https://www.acmicpc.net/problem/2749

2749번: 피보나치 수 3

 

 

풀이 과정

[피사노 주기 문제]   [행렬 풀이 코드 1]   [행렬 풀이 코드 2]   [피보나치의 행렬 멱법]

해당 문제를 직접 풀지 못하고 다른 사람들의 풀이를 찾아보게 되었다. 풀이는 크게 두 가지였다. 하나는 피사노 주기를 이용하는 방법과 다른 하나는 행렬을 이용하는 방법이었다. 필자는 위의 링크들을 참고하여 행렬을 이용한 풀이를 선택했다. 피사노 주기에 대한 풀이가 훨씬 간단했지만, 해당 조건보다 행렬을 이용해 문제를 풀이하는 방법이 더 보편적이고 다른 문제에도 적용할 수 있을 것이라고 생각했다.

 

바로 전날 풀이했던 행렬 제곱 문제의 코드를 거의 다시 사용하여 작성할 수 있었다.

 

피보나치수열의 경우 아래 형태와 같이 행렬 멱법을 통해 나타낼 수 있다.

출처 : https://zzonglove.tistory.com/32

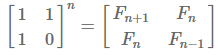
피보나치수열의 반복되는 특성상 피보나치 수를 행렬의 거듭제곱 형태로 표현할 수 있고, 거듭제곱 형태의 행렬 곱은 분할 정복 알고리즘을 통해 O(logN)의 시간 복잡도로 문제를 해결할 수 있기 때문에 해당 문제를 제한 시간 안에 풀 수 있게 된다.

 

 

소스 코드

#include <iostream>
#include <cstring>
#define div_n 1000000
using namespace std;

long long N;

long long A[2][2]={{1,1}, {1,0}};
long long ans[2][2];

void mat_mul(long long a[2][2], long long b[2][2]){
    long long temp[2][2];
    memset(temp, 0, sizeof(temp));
    for(int i=0;i<2;i++){
        for(int j=0;j<2;j++){
            for(int k=0;k<2;k++){
                temp[i][j] += a[i][k]*b[k][j];
            }
            temp[i][j] = temp[i][j] % div_n;
        }
    }

    memcpy(a,temp,sizeof(temp));
}

void power(long long n){
    while(n>0){
        if(n%2==1){
            mat_mul(ans,A);
        }
        mat_mul(A,A);
        n /= 2;
    }
}


int main(){
    cin >> N;
    for(int i=0;i<2;i++){
        ans[i][i]=1;
    }
    power(N);
    cout << ans[1][0] % div_n;
    return 0;
}

 

결과 및 후기

알고리즘 문제들을 풀어보면서 행렬(배열)을 이용한 문제를 많이 풀어보았지만 선형 대수적인 행렬을 적용하여 문제를 풀어서 새로웠다. 그리고 현재 선형대수의 지식이 부족하다는 것을 느낄 수 있는 문제였다.